1 Definiciones

Un objeto 3D está compuesto de una o más mallas (meshes en inglés)

Una malla es una colección de vértices, aristas, y caras (vertices, edges, y faces)

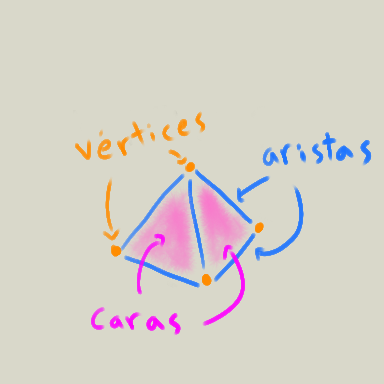
Los vértices son puntos, posiciones en el espacio 3D, que además pueden contener información como color o coordenada de alguna textura.

Las aristas son la conexión o relación entre dos vértices.

Las caras son un conjunto cerrado de aristas. Generalmente tienen forma triangular o cuadrangular (quad).

El método que utilizaremos para definir mallas en Processing se llama Cara-vértice (Face-vertex): Definiremos cuál es nuestro conjunto de vértices, y definiremos cuáles son las caras que dichos vértices conforman.

2 Modos de dibujo con beginShape()

Para dibujar nuestras propias mallas en Processing, necesitamos hacer uso de las funciones beginShape() y endShape(), que nos permiten agrupar en caras un conjunto de vértices descritos por la función vertex().

Los siguientes modos de dibujo le indican a Processing cómo queremos que se conecten los vértices, dando paso a aristas y caras:

• TRIANGLES
• QUADS
• TRIANGLE_STRIP
• TRIANGLE_FAN
• QUAD_STRIP

(El nombre es así, todo en mayúsculas)

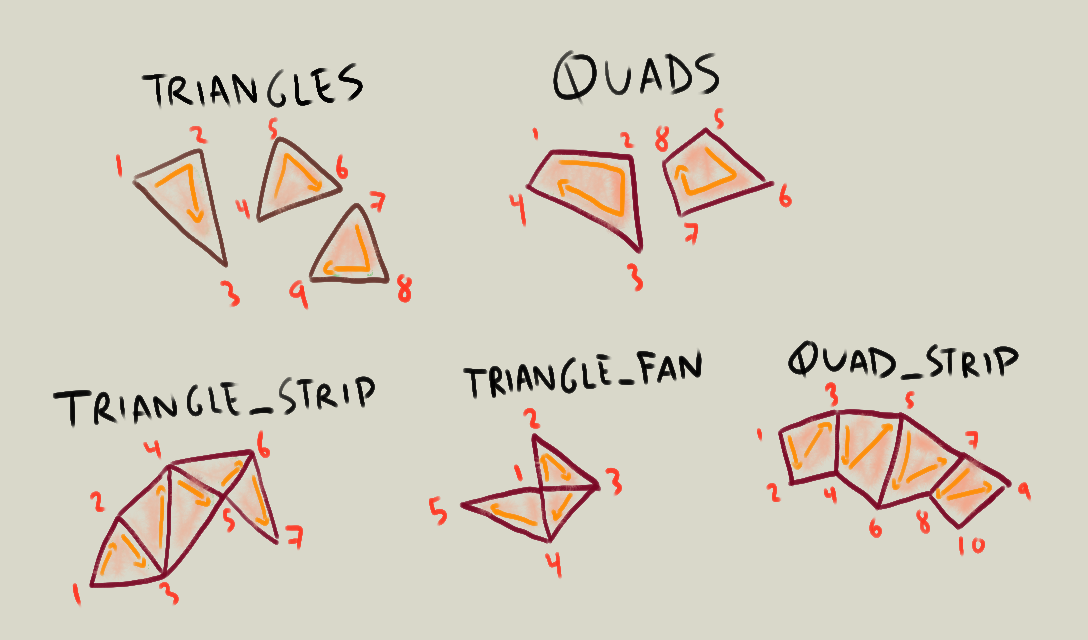
2.1 TRIANGLES y QUADS

Estos dos modos de dibujo son los básicos, con los que conviene empezar a trabajar.

• En el caso de TRIANGLES, cada grupo de tres vértices se agrupa como una cara triangular.
• En el caso de QUADS cada grupo de cuatro vértices se agrupa como una cara cuadrangular.

Se recomienda que el orden de los vértices se coloque en la dirección de las manecillas del reloj (CW: Clockwise).

Con estos modos “no hay pierde”. El único inconveniente es que cuando queremos hacer mallas más complicadas, donde hay vértices que le pertenecen a más de una cara, usar estos dos modos nos hará tener muchas declaraciones vertex() repetidas.

2.2 TRIANGLE_STRIP, TRIANGLE_FAN, y QUAD_STRIP

Estos modos de dibujo son un poco más complejos de utilizar, pero tienen la ventaja de que en mallas complicadas podemos ahorrarnos líneas de código.

• TRIANGLE_STRIP: Cada nuevo vértice que se declare va a formar una cara triangular con los dos vértices anteriores.
• TRIANGLE_FAN: Cada nuevo vértice que se declare va a formar una cara triangular con el vértice anterior, y con el primer vértice de la malla. El primer vértice de la malla se vuelve el “centro” al que todos los triángulos convergen.
• QUAD_STRIP: Cada par de vértices nuevos que se declaren, van a formar una cara cuadrangular con los dos vértices antriores.

En la ilustración, vemos que el ejemplo de TRIANGLE_STRIP tiene 5 triángulos y 7 vértices. Crear esa figura con TRIANGLE_STRIP solo requiere escribir 7 líneas de vertex(), mientras que crearla con TRIANGLES requeriría 15 líneas de vertex().

3 PVector como vértices

Podemos utilizar la clase PVector para almacenar y eventualmente manipular vértices 3D.

La forma de declararlos:

PVector punto1 = new PVector( 0, 10, 5); // crea el vértice punto1 en (0,10,5)
PVector punto2 = new PVector( 1, 1, 1); // crea el vértice punto2 en (1,1,1)
PVector punto3 = new PVector( 10, 50, 10); // crea el vértice punto3 en (10,50,10)

La forma de utilizarlos como vértices dentro de beginShape():

beginShape(TRIANGLES);
vertex(punto1.x, punto1.y, punto1.z);
vertex(punto2.x, punto2.y, punto2.z);
vertex(punto3.x, punto2.y, punto3.z);
endShape();

Es posible usar los métodos add() y sub() para incrementar o decrementar los valores x,y,z del vértice:

punto1.add(0, 2, 0); // súmale 2 unidades en Y al punto1
punto1.sub(1, 0, 0); // réstale 1 unidad en X al punto1

4 Ejemplo: Pirámide

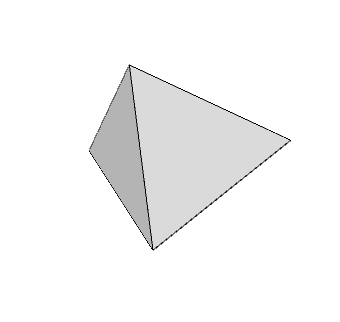
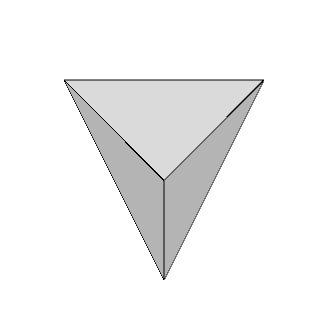
Como primer ejemplo de malla, construimos una pirámide triangular.

4.1 Boceto

Partimos de un boceto para ubicar vértices y caras:

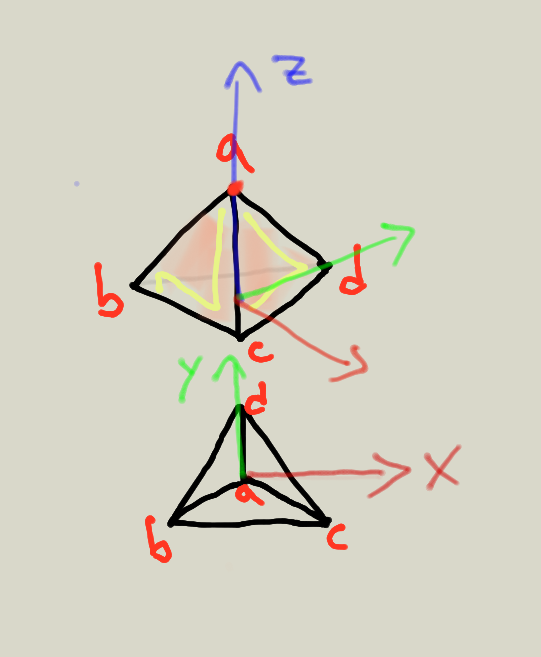
4.2 Identificación de vértices y caras

Los cuatro vértices que tiene la malla son: a, b, c, d

Las cuatro caras con las que cuenta la pirámide son, con los vértices escritos en la dirección de las manecillas del reloj (clockwise)

• acb
• adc
• abd
• bcd

4.3 Pirámide con TRIANGLES

El modo de dibujo TRIANGLES crea un triángulo por cada tres vértices (vertex()) que coloquemos.

Es el método más claro para dibujar una malla, pero puede implicar repetir múltiples llamadas a los mismos vértices.

void piramide(){
  // Define vertices
  PVector a = new PVector(0,0,1);
  PVector b = new PVector(-1,-1,0);
  PVector c = new PVector(1,-1,0);
  PVector d = new PVector(0,1,0);

  // Define caras (TRIANGLES)
  beginShape(TRIANGLES);
  // cara acb
  vertex( a.x, a.y, a.z );
  vertex( c.x, c.y, c.z );
  vertex( b.x, b.y, b.z );

  // cara adc
  vertex( a.x, a.y, a.z);
  vertex( d.x, d.y, d.z);
  vertex( c.x, c.y, c.z);

  // cara abd
  vertex( a.x, a.y, a.z);
  vertex( b.x, b.y, b.z);
  vertex( d.x, d.y, d.z);

  // cara dbc
  vertex(d.x, d.y, d.z);
  vertex(b.x, b.y, b.z);
  vertex(c.x, c.y, c.z);
  endShape();
}

4.4 Pirámide con TRIANGLE_FAN

Podemos notar que la parte superior de la pirámide consiste en tres triángulos que en común tienen el vértice a, y que esto se parece al modo de dibujo TRIANGLE_FAN.

Entonces, toda esa sección superior puede construirse de la siguiente forma:

  beginShape(TRIANGLE_FAN);
  vertex(a.x, a.y, a.z); // punto central, común entre todos los triángulos
  vertex(d.x, d.y, d.z);
  vertex(c.x, c.y, c.z); // termina triángulo a-d-c
  vertex(b.x, b.y, b.z); // agrega triángulo b-a-c
  vertex(d.x, d.y, d.z); // agrega triángulo d-a-b
  endShape();

Son menos líneas de código, pero un poco más difícil de leer. Además, la cara inferior de la pirámide no entra en el patrón, por lo que hay que dibujarla aparte.

La función completa quedaría así:

void piramide(){
  // Vertices
  PVector a = new PVector(0,0,1);
  PVector b = new PVector(-1,-1,0);
  PVector c = new PVector(1,-1,0);
  PVector d = new PVector(0,1,0);
  
  // Caras
  // caras parte superior
  beginShape(TRIANGLE_FAN);
  vertex(a.x, a.y, a.z);
  vertex(d.x, d.y, d.z);
  vertex(c.x, c.y, c.z); // termina triángulo c-a-d
  vertex(b.x, b.y, b.z); // agrega triángulo b-a-c
  vertex(d.x, d.y, d.z); // agrega triángulo d-a-b
  endShape();

  // cara base
  beginShape(TRIANGLES);
  vertex(d.x, d.y, d.z);
  vertex(b.x, b.y, b.z);
  vertex(c.x, c.y, c.z);
  endShape();
}

5 Construyendo una malla (manualmente)

Para construir una malla asignando los vértices y las caras de manera manual, sugiero llevar a cabo los siguientes pasos:

• Boceto(s) de malla
• Identificación de vértices
• Identificación de aristas y caras
• Codificación

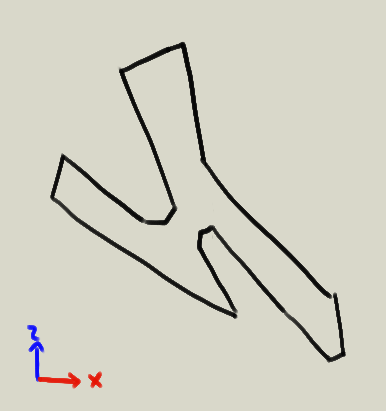
5.1 Boceto(s) de malla

Como hemos visto en otras ocasiones, conviene tener a la mano al menos una proyección paralela de lo que queremos construir.

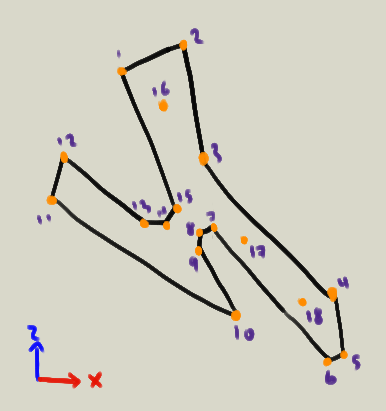
5.2 Identificación de vértices

Al identificar los vértices, hay que nombrarlos/numerarlos, y encontrar su ubicación 3D (aproximada o no, tomando en cuenta que las posiciones se pueden ajustar en el código).

Si el boceto tiene líneas curvas, hay que asignar algunos vértices para aproximarlas.

En el código los declararemos como variables de tipo PVector (PVector como Vértices)

5.3 Identificación de aristas y caras

Este proceso también se llama teselación. En nuestro caso, buscamos identificar caras triangulares y/o cuadrangulares (quads), formadas a partir de conectar vértices con aristas.

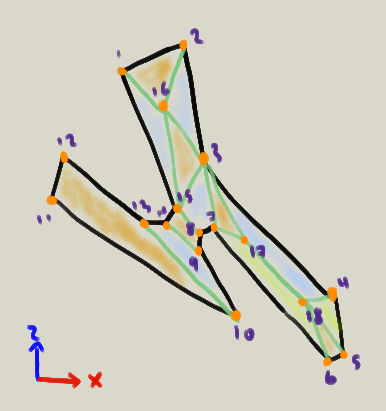
Conviene tomar en cuenta los Modos de dibujo en beginShape(), por si podemos/queremos hacer que nuestra teselación quede parcial o completamente descrita por los modos TRIANGLE_STRIP, TRIANGLE_FAN, o QUAD_STRIP, para escribir menos código.

Si no, no hay problema, y podemos definir todas las caras como triángulos (TRIANGLES) o quads (QUADS) individuales.

5.4 Codificación

Ya que tenemos todos nuestros elementos - vértices nombrados/numerados y con posición, y caras definidas - podemos pasar a escribirlos en Processing. Como referencia, tenemos la Pirámide de arriba.

6 Apariencia: Texturas

[P3D: Texturas en Mallas]