Tutorial: Copos y flores (Funciones y transformaciones)
Este tutorial es un ejemplo sencillo que realiza a la siguiente actividad:
ACTIVIDAD: Copos de nieve, flores, y más
Donde el objetivo es realizar una composición visual basada en una función propia con parámetros que construya una flor/copo de nieve/etc a partir de la rotación de pétalos construidos con otra función propia.
1 Diseño del pétalo
Boceteamos e implementamos una figura pétalo con su base (punto de rotación) en las coordenadas 0,0.
Por ejemplo, la siguiente es una línea vertical acompañada de cuatro líneas diagonales
line(0,0, 0, d);
line(0,d, -20, d+20);
line(0,d, 20, d+20);
line(0,d/2, -20, d/2+20);
line(0,d/2, 20, d/2+20);
Nota que hay un parámetro d que se refiere al largo de la línea.
2 Función de dibujo del pétalo
Podemos agrupar el código dentro de una función propia con un parámetro d:
void petalo( float d ){
// dibuja un pétalo con largo 'd'
line(0,0, 0, d);
line(0,d, -20, d+20);
line(0,d, 20, d+20);
line(0,d/2, -20, d/2+20);
line(0,d/2, 20, d/2+20);
}Esta función, en contexto de todo el programa, se vería así:
void setup() {
size(500, 500);
background(0);
stroke(255);
strokeWeight(5);
}
void draw() {
// dibuja un pétalo con largo 100
petalo( 100 );
}
void petalo(float d) {
// dibuja un pétalo con largo 'd'
line(0, 0, 0, d);
line(0, d, -20, d+20);
line(0, d, 20, d+20);
line(0, d/2, -20, d/2+20);
line(0, d/2, 20, d/2+20);
}Nota que con el programa en esa forma, el pétalo se dibuja con su base en 0,0 y se ve incompleto.
3 Transformaciones
3.1 Traslación
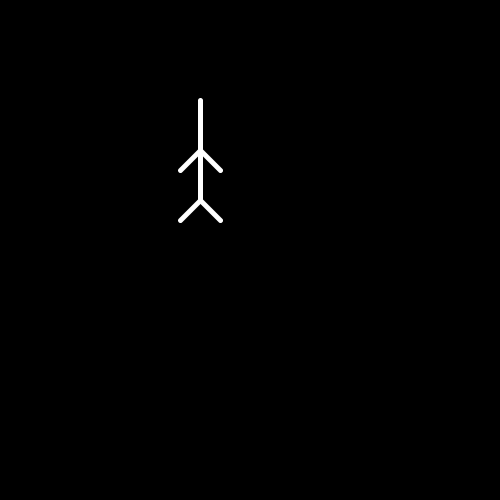
Para dibujar el pétalo con su base en otra posición, podemos utilizar translate( ), que cambia la posición del origen. Solamente enfocándonos en la función draw():
void draw() {
// mueve el origen 200 pixeles a la derecha
// y 100 pixeles hacia abajo:
translate( 200, 100 );
// dibuja un pétalo con largo 100
petalo( 100 );
}
3.2 Repetición y rotación
La función rotate( ) va a rotar el lienzo usando al origen como punto del eje de rotación.
Dibujar la punta de nuestro pétalo respecto a 0,0 nos facilita usar esa punta como posición del eje de rotación.
Lo añadido a continuación repite 5 veces una rotación, donde en cada rotación se gira 360/5 grados:
void draw() {
// mueve el origen 200 pixeles a la derecha
// y 100 pixeles hacia abajo:
translate( 200, 100 );
// repite 5 veces lo siguiente:
for(int i=0; i<5; i=i+1){
petalo( 100 ); // dibuja el pétalo
rotate( radians( 360/5 ) ); // rota 360/5 grados
}
}
3.3 Guardado y recuperación del origen
Es buena práctica siempre preceder cualquier grupo de transformaciones con pushMatrix() y terminarlas con popMatrix() para que lo que dibujemos después parta de un origen en 0,0 y un lienzo sin rotaciones ni escalamientos:
void draw() {
// guarda el origen
pushMatrix();
// mueve el origen 200 pixeles a la derecha
// y 100 pixeles hacia abajo:
translate( 200, 100 );
// repite 5 veces lo siguiente:
for(int i=0; i<5; i=i+1){
petalo( 100 ); // dibuja el pétalo
rotate( radians( 360/5 ) ); // rota 360/5 grados
}
// recupera el origen
popMatrix();
}4 Función de dibujo de la flor
A partir de lo anterior, podemos identificar que la función de translate( ) coloca el centro de nuestro copo/flor en la posición que deseemos.
Agrupamos todo ese código dentro de una función flor( ) con dos parámetros, x y y. Nosotras les asignamos nombre y orden dentro de los argumentos de nuestra función.
Nota que esas variables reemplazan a los valores previos de 200 y 100 dentro de translate( ):
void flor( float x, float y) {
// dibuja una flor con centro en x, y
// guarda el origen
pushMatrix();
// mueve el origen x pixeles a la derecha
// y pixeles hacia abajo:
translate( x, y );
// repite 5 veces lo siguiente:
for(int i=0; i<5; i=i+1){
petalo( 100 ); // dibuja el pétalo
rotate( radians( 360/5 ) ); // rota 360/5 grados
}
// recupera el origen
popMatrix();
}Podemos llamar esta función dentro de draw() para dibujar la flor en coordenadas específicas.
4.1 En contexto
Este programa dibuja una flor en el centro del lienzo:
void setup() {
size(500, 500);
background(0);
stroke(255);
strokeWeight(5);
}
void draw() {
// dibuja una flor en el centro del lienzo
flor( width/2, height/2 );
}
void flor( float x, float y) {
// dibuja una flor con centro en x, y
// guarda el origen
pushMatrix();
// mueve el origen x pixeles a la derecha
// y pixeles hacia abajo:
translate( x, y );
// repite 5 veces lo siguiente:
for(int i=0; i<5; i=i+1){
petalo( 100 ); // dibuja el pétalo
rotate( radians( 360/5 ) ); // rota 360/5 grados
}
// recupera el origen
popMatrix();
}
void petalo(float d) {
// dibuja un pétalo con largo 'd'
line(0, 0, 0, d);
line(0, d, -20, d+20);
line(0, d, 20, d+20);
line(0, d/2, -20, d/2+20);
line(0, d/2, 20, d/2+20);
}
5 Función de dibujo con más parámetros: largo y repeticiones
La función anterior siempre dibujará una flor de 5 pétalos de 100 pixeles de largo.
Para tener más flexibilidad, podemos agregar esas cantidades como parámetros: d será el largo del pétalo y n el número de pétalos. Esos nombres los decidimos tanto en nombre como en orden dentro de la lista de parámetros.
Nota cómo estas variables reemplazan las cantidades que previamente eran números literales:
void flor( float x, float y, float d, int n) {
// dibuja una flor con:
// x,y: coordenadas del centro
// d: largo de petalo
// n: número de pétalos
// guarda el origen
pushMatrix();
// mueve el origen x pixeles a la derecha
// y pixeles hacia abajo:
translate( x, y );
// repite n veces lo siguiente:
for(int i=0; i<n; i=i+1){
petalo( d ); // dibuja el pétalo de largo d
rotate( radians( 360/n ) ); // rota 360/n grados
}
// recupera el origen
popMatrix();
}5.1 En contexto
Con esta nueva función, podemos dibujar flores en distintas posiciones, de distintos tamaños, y con distinto número de pétalos:
void setup() {
size(500, 500);
background(0);
stroke(255);
strokeWeight(5);
}
void draw() {
// flor en el centro del lienzo, tamaño 120, 8 pétalos
flor(width/2, height/4, 120, 8);
// flor abajo a la izquierda, tamaño 50, 10 pétalos
flor(width/4, height*3/4, 50, 10);
// flor abajo a la derecha, tamaño 80, 5 pétalos
flor(width*3/4, height*3/4, 80, 5);
}
void flor( float x, float y, float d, int n) {
// dibuja una flor con:
// x,y: coordenadas del centro
// d: largo de petalo
// n: número de pétalos
// guarda el origen
pushMatrix();
// mueve el origen x pixeles a la derecha
// y pixeles hacia abajo:
translate( x, y );
// repite n veces lo siguiente:
for(int i=0; i<n; i=i+1){
petalo( d ); // dibuja el pétalo de largo d
rotate( radians( 360/n ) ); // rota 360/n grados
}
// recupera el origen
popMatrix();
}
void petalo(float d) {
// dibuja un pétalo con largo 'd'
line(0, 0, 0, d);
line(0, d, -20, d+20);
line(0, d, 20, d+20);
line(0, d/2, -20, d/2+20);
line(0, d/2, 20, d/2+20);
}