Coordenadas polares
1 Fundamentos
El sistema de coordenadas polares es un sistema de coordenadas en dos dimensiones donde cada punto se ubica a partir de un valor de radio r (distancia respecto a un punto de referencia) y de ángulo a (respecto a una dirección de referencia).
1.1 Conversión a coordenadas rectangulares
Para convertir de coordenadas polares a rectangulares, usamos funciones trigonométricas pues relacionan un radio (hipotenusa) y ángulo, con los lados (catetos) de un triángulo rectángulo.
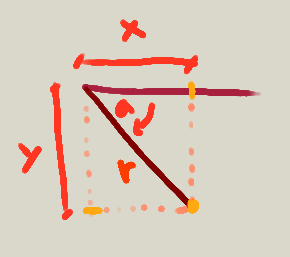
Estas son las fórmulas para convertir coordenadas polares r,a con centro en cx,cy, a coordenadas rectangulares x,y.
// calcula coordenadas rectangulares x,y a partir de:
// r: radio
// a: ángulo
// cx,cy: centro / punto de referencia
float x = r*cos(a) + cx;
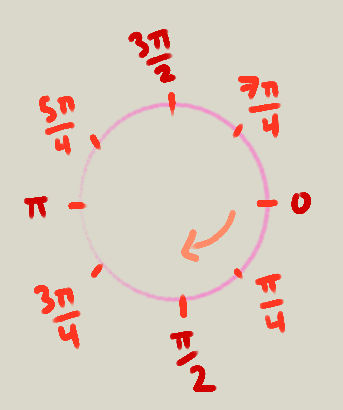
float y = r*sin(a) + cy;El siguiente diagrama muestra algunos valores comunes de ángulos medidos en radianes:
2 Ejemplos de código: radio constante
Los siguientes son sketches de código que demuestran varias posibilidades de utilizar coordenadas polares de manera tradicional con un valor de radio constante y un ángulo que avanza de 0 a TWO_PI.
2.1 Polígono regular
Este ejemplo dibuja un polígono regular a partir de calcular la posición de sus vértices con coordenadas polares.
Nota cómo al cambiar el divisor del incremento del ángulo, aumentarás o reducirás el número de lados.
size(400, 400);
background(0);
noFill();
stroke(255);
beginShape();
// cambia el ángulo en incrementos de TWO_PI/6
for(float a=0; a<=TWO_PI; a=a+TWO_PI/6){
// calcula las coordenadas x,y con radio 100 y centro en 200,200
float x = 100*cos(a) + 200;
float y = 100*sin(a) + 200;
// establece el vértice del polígono en x,y
vertex(x,y);
}
endShape(CLOSE);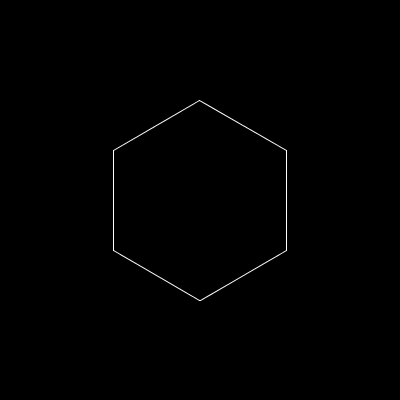
2.2 Rayos/Radios
Este ejemplo dibuja 16 líneas que van hacia el centro desde puntos ubicados en una circunferencia.
size(400, 400);
background(0);
noFill();
stroke(255);
// aumenta el ángulo en incrementos de TWO_PI/16
for(float a=0; a<=TWO_PI; a=a+TWO_PI/16){
// calcula las coordenadas x,y con radio 100 y centro en 200,200
float x = 100*cos(a) + 200;
float y = 100*sin(a) + 200;
// dibuja una línea del punto x,y al centro
line(x,y, 200, 200);
}
2.3 Aleatoriedad en área circular
Este ejemplo dibuja 500 puntos en posición aleatoria dentro de un área circular de 100 pixeles de radio y centro en 200,200.
Para que los puntos estén dentro de esa área, en vez de generar coordenadas x,y aleatorias se generan un radio r y un ángulo a aleatorios. Estas coordenadas polares entonces se usan para calcular las coordenadas x,y correspondientes.
size(400, 400);
background(0);
noFill();
stroke(255);
strokeWeight(5);
// repite 500 veces:
for(int cuenta=1; cuenta<=500; cuenta++){
// genera un radio aleatorio entre 0 y 100
float r = random(0, 100);
// genera un ángulo aleatorio entre 0 y TWO_PI
float a = random(0, TWO_PI);
// calcula coordenadas x,y
// en función de r, a
float x = r*cos(a) + 200;
float y = r*sin(a) + 200;
// dibuja punto en x,y
point(x,y);
}
2.4 Curva de Lissajous
Este es un caso especial de uso de coordenadas polares, en el que la posición de cada vértice x,y de una figura se basa en dos funciones senoidales con frecuencia distinta.
En este ejemplo, esas frecuencias son de 3 y 4.
Prueba cambiar esas cantidades para obtener otras versiones.
size(400, 400);
background(0);
noFill();
stroke(255);
beginShape();
for(float a=0; a<=TWO_PI; a=a+PI/100){
float x = 100*sin(3*a) + 200;
float y = 100*sin(4*a) + 200;
vertex(x,y);
}
endShape(CLOSE);
3 Ejemplos de código: radio variable
En estos ejemplos el radio de una figura circular cambia con cada iteración del ciclo for.
Todos usan vertex(x,y) para definir los vértices de un polígono entre beginShape() y endShape().
3.1 Espiral
En este ejemplo tenemos una variable r que funciona como acumulador y que corresponde a la longitud del radio. En cada iteración del ciclo aumenta un poco, por lo que cada vértice está más alejado del punto central respecto a los anteriores.
Nota que en el ciclo for la condición while indica que las repeticiones sucederán mientras el ángulo sea menor o igual a 5*TWO_PI; es decir, el ángulo dará 5 vueltas.
Prueba cambiar ese número de vueltas y/o los incrementos al radio y al ángulo en cada iteración.
size(400, 400);
background(0);
noFill();
stroke(255);
beginShape();
// valor inicial del radio
float r = 1;
// itera con un ángulo entre 0 y 5*TWO_PI
for(float a=0; a<=5*TWO_PI; a=a+PI/100){
// calcula coordenadas rectangulares
float x = r*cos(a) + 200;
float y = r*sin(a) + 200;
vertex(x,y);
// en cada iteración el radio aumenta linealmente
r = r + 0.1;
}
endShape();
[Variables: Contadores, Acumuladores, Banderas]
3.2 Flores
En este ejemplo la longitud del radio cambia de acuerdo a una función senoidal, a una frecuencia mayor que las funciones seno y coseno que utilizamos para calcular las posiciones de los vértices.
Prueba modificar la amplitud de esa función del radio, su frecuencia, e incluso su punto central.
size(500, 500);
background(0);
noFill();
stroke(255);
beginShape();
for(float a=0; a<=TWO_PI; a=a+PI/1000){
// la longitud del radio oscila de -200 a 200
// realizando 8 ciclos por cada ciclo de 'a'
float r = 200*sin(8*a);
float x = r*cos(a) + 250;
float y = r*sin(a) + 250;
vertex(x,y);
}
endShape(CLOSE);
3.3 Aleatorio
En este ejemplo cada vértice tiene un radio distinto generado de manera aleatoria.
Prueba modificar el incremento de ángulo en el ciclo y/o el rango aleatorio del radio.
size(400, 400);
background(0);
noFill();
stroke(255);
beginShape();
for(float a=0; a<=TWO_PI; a=a+PI/100){
// genera un radio aleatorio para cada punto
float r = random(50, 150);
float x = r*cos(a) + 200;
float y = r*sin(a) + 200;
vertex(x,y);
}
endShape();
3.4 Y más…
Estos ejemplos solo son algunas sugerencias de posibilidades. Te invito a experimentar combinándolos o haciéndolos más complejos.