jardínBit

Funciones trigonométricas

Las funciones trigonométricas definen relaciones entre los lados y ángulos de un triángulo rectángulo.

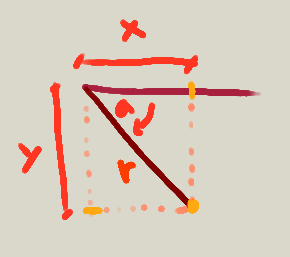
sin( a ) <-> y/r
cos( a ) <-> x/r
tan( a ) <-> y/x

[Ángulos en radianes]

1 Seno y coseno

Estas dos funciones son periódicas y tienen un rango de resultados entre -1 y 1.

Suelen usarse para generar comportamientos oscilatorios y para trabajar con coordenadas polares.

[Coordenadas polares]

Las dos funciones tienen la misma forma pero están desfasadas por HALF_PI.

1.1 En función del espacio

Estos ejemplos utilizan ciclos for para dibujar un conjunto de puntos.

[Ciclos while y for]

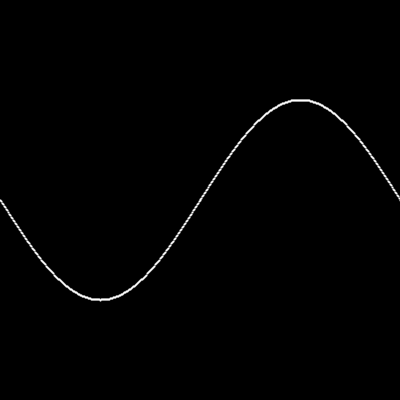
El siguiente programa dibuja a la función sin( ) con un periodo correspondiente al canvas completo:

size(400, 400);
background(0);
stroke(255);
strokeWeight(2);

for(float x=0; x<=width; x++){
 float y = 100*sin( TWO_PI*x/width ) + 200;
 point(x,y);  
}

Algunas observaciones y definiciones:

Podemos obtener el mismo dibujo utilizando la función map( ):

// dibuja 1 ciclo de la función seno
size(400, 400);
background(0);
stroke(255);
strokeWeight(2);

for(float x=0; x<=width; x++){
 // convierte a x 
 // que tiene un rango original de 0 a width
 // a un rango entre 0 y TWO_PI
 float t = map(x, 0, width, 0, TWO_PI);

 // convierte al resultado de sin(t)
 // que tiene un rango original entre -1 y 1
 // a un rango entre 100 y 300
 float y = map( sin(t), -1, 1,  100, 300);
 point(x,y);  
}

[Mapeo/conversión de valores]

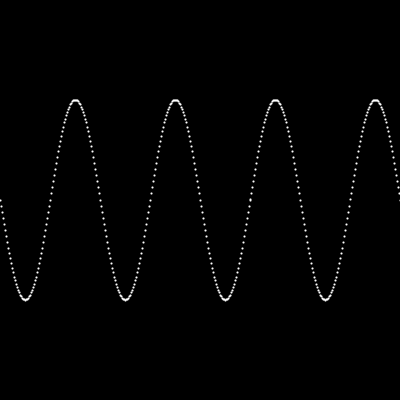
En el siguiente ejemplo, lo único que cambia es la frecuencia, de TWO_PI a 4*TWO_PI. Nota cómo ahora hay cuatro ciclos:

// dibuja 4 ciclos de la función seno
size(400, 400);
background(0);
stroke(255);
strokeWeight(2);

for(float x=0; x<=width; x++){
 // convierte a x 
 // que tiene un rango original de 0 a width
 // a un rango entre 0 y 4*TWO_PI
 float t = map(x, 0, width, 0, 4*TWO_PI);

 // convierte al resultado de sin(t)
 // que tiene un rango original entre -1 y 1
 // a un rango entre 100 y 300
 float y = map( sin(t), -1, 1,  100, 300);
 point(x,y);  
}

1.2 En función del tiempo

Estos ejemplos utilizan el ciclo de animación para funcionar.

[Ciclo de animación]

En este ejemplo el brillo del fondo es modulado por una función senoidal.

void setup(){
 size(400, 400); 
}

void draw(){

 // un ciclo completo sucede en 300 frames
 // el rango del brillo irá de 0 a 256
 float brillo = 128*sin( TWO_PI*frameCount/300) + 128;

 // asigna el resultado al color de fondo
 background(brillo);
}

Alternativamente, podríamos utilizar la función `map( ) para establecer la escala del tiempo y de la amplitud:

void setup(){
 size(400, 400); 
}

void draw(){
 // convierte frameCount
 // de un rango original de 0 a 300 frames
 // a un rango de 0 a TWO_PI
 // (hace que un ciclo completo suceda en 300 frames)
 float t = map(frameCount, 0, 300, 0, TWO_PI);
 
 // convierte el resultado de sin(t)
 // de un rango de -1 a 1
 // a uno de 0 a 255
 float brillo = map( sin(t), -1, 1, 0, 255);
 // asigna el resultado al color de fondo
 background(brillo);
}

Nota: si bien frameCount sigue incrementándose más allá de 300, la función map() se encarga de seguirlo convirtiendo con la misma relación de 300 frames a TWO_PI