P3D: Sólidos cilíndricos y cónicos
1 Coordenadas polares
Las siguientes funciones se basan en la herramienta de las coordenadas polares, con las que en lugar de ubicar un punto de acuerdo a coordenadas x, y, z (distancia al origen paralela a cad eje), lo ubicamos de acuerdo a un radio (distancia al centro) y a un ángulo respecto a una referencia.
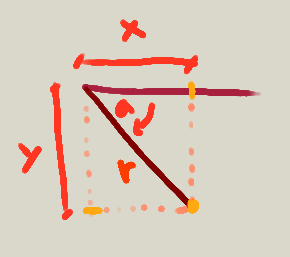
Estas son las fórmulas para convertir coordenadas polares r,a con centro en cx,cy, a coordenadas rectangulares x,y.
// calcula coordenadas rectangulares x,y a partir de:
// r: radio
// a: ángulo
// cx,cy: centro / punto de referencia
float x = r*cos(a) + cx;
float y = r*sin(a) + cy;2 Ejemplos de mallas cónicas
Las siguientes funciones aprovechan el modo de dibujo TRIANGLE_FAN y la conversión de coordenadas polares a rectangulares para dibujar distintas mallas cónicas.
2.1 Cono tradicional

Esta función dibuja un cono de radio r, altura h, y una base con N lados.
void cono(float r, float h, int N){
// dibuja un cono tradicional
// r: radio de la base
// h: altura
// N: número de divisiones en la base
// variables auxiliares:
float x,y;
beginShape(TRIANGLE_FAN);
vertex(0,0,h); // vértice de la punta
// ciclo para los vértices de la base
for(float angulo=0; angulo<=TWO_PI; angulo=angulo+TWO_PI/N){
x = r*cos(angulo);
y = r*sin(angulo);
vertex(x,y,0);
}
endShape();
}2.2 Cono con base aleatoria
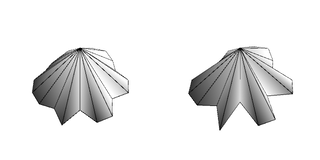
Aquí se le suma o resta una cantidad aleatoria al radio que le corresponde a cada vértice.
Los parámetros son el radio r, altura h, una base con N lados, y un rango de cuánto puede variar el radio.
void cono(float r, float h, int N, float rango){
// dibuja un cono con base pseudoaleatoria
// r: radio de la base
// h: altura
// N: número de divisiones en la base
// rango: cuánto puede variar el radio hacia arriba y hacia abajo
int seed = 100;
randomSeed(seed);
// variables auxiliares:
float x,y,angulo,radio;
beginShape(TRIANGLE_FAN);
vertex(0,0,h); // vértice de la punta
// ciclo para los vértices de la base
for(int i=0;i<=N;i=i+1){
angulo = i*TWO_PI/N;
radio = r + random(-rango, rango);
x = radio*cos(angulo);
y = radio*sin(angulo);
vertex(x,y,0);
if(i==N-1){ randomSeed(seed); }
}
endShape();
}2.3 Cono con base periódica

En este ejemplo se utiliza una función senoidal para ir cambiando de manera continua y periódica la magnitud del radio.
Los parámetros son el radio r, altura h, una base con N lados, un rango de cuánto puede variar el radio, y un número de ciclos/picos nciclos que existirán en la base.
void cono(float r, float h, int N, float rango, int nciclos){
// dibuja un cono con base periódica
// r: radio de la base
// h: altura
// N: número de divisiones en la base
// rango: cuánto puede variar el radio hacia arriba y hacia abajo
// nciclos: cuántos ciclos/picos tiene la base
// variables auxiliares:
float x,y,angulo,radio;
beginShape(TRIANGLE_FAN);
vertex(0,0,h); // vértice de la punta
// ciclo para los vértices de la base
for(int i=0;i<=N;i=i+1){
angulo = i*TWO_PI/N;
radio = r + rango*sin( i*TWO_PI*nciclos/N );
x = radio*cos(angulo);
y = radio*sin(angulo);
vertex(x,y,0);
}
endShape();
}3 Ejemplos de mallas cilíndricas
En estos ejemplos se aprovecha el modo de dibujo QUAD_STRIP y la conversión de coordenadas polares a rectangulares para establecer mallas cilíndricas.
3.1 Cilindro tradicional

Esta función recibe tres parámetros: r para el radio, h para la altura, y N para el número de lados en la base/tapa.
void cilindro(float r, float h, int N){
// dibuja un cilindro tradicional
// r: radio de la base
// h: altura
// N: número de divisiones en la base
// variables auxiliares
float x,y;
beginShape(QUAD_STRIP);
for(float angulo=0; angulo<=TWO_PI; angulo=angulo+TWO_PI/N){
x = r*cos(angulo);
y = r*sin(angulo);
// vértice en la base
vertex(x,y,0);
// vértice en la tapa
vertex(x,y,h);
}
endShape();
}3.1.1 Variación: Cilindro con rango de ángulo
Esta función permite determinar el ángulo de inicio y fin del cilindro. Nota que los ángulos se especifican en radianes.
void cilindro(float r, float h, int N, float anguloInicial, float anguloFinal){
// dibuja un cilindro tradicional, en un rango específico de ángulo
// r: radio de la base
// h: altura
// N: número de divisiones en la base
// anguloInicial: a partir de qué ángulo empieza el cilindro (en radianes)
// anguloFinal: en qué ángulo termina el cilindro (en radianes)
// variables auxiliares
float x,y;
beginShape(QUAD_STRIP);
for(float angulo=anguloInicial; angulo<=anguloFinal; angulo += (anguloFinal-anguloInicial)/N){
x = r*cos(angulo);
y = r*sin(angulo);
// vértice en la base
vertex(x,y,0);
// vértice en la tapa
vertex(x,y,h);
}
endShape();
}3.2 Cilindro con base/tapa aleatoria

Esta función recibe cuatro parámetros: r para el radio, h para la altura, N para el número de lados en la base/tapa, y rango para cuánto puede variar el radio.
void cilindro(float r, float h, int N, float rango){
// dibuja un cilindro con base pseudoaleatoria
// r: radio de la base
// h: altura
// N: número de divisiones en la base
// rango: cuánto puede variar el radio hacia arriba y hacia abajo
// variables auxiliares
float x,y,angulo,radio;
int seed = 100;
randomSeed(seed);
beginShape(QUAD_STRIP);
for(int i=0; i<=N; i=i+1){
angulo = i*TWO_PI/N;
radio = r + random(-rango, rango);
x = radio*cos(angulo);
y = radio*sin(angulo);
// vértice en la base
vertex(x,y,0);
// vértice en la tapa
vertex(x,y,h);
if(i==N-1){ randomSeed(seed); }
}
endShape();
}3.3 Cilindro con base/tapa periódica

Esta función recibe cinco parámetros: r para el radio, h para la altura, N para el número de lados en la base/tapa, rango para cuánto puede variar el radio, y nciclos para indicar cuántos picos tendrá la base/tapa.
void cilindro(float r, float h, int N, float rango, int nciclos){
// dibuja un cilindro con base periódica
// r: radio de la base
// h: altura
// N: número de divisiones en la base
// rango: cuánto puede variar el radio hacia arriba y hacia abajo
// nciclos: cuántos ciclos/picos tiene la base
// variables auxiliares
float x,y,angulo,radio;
beginShape(QUAD_STRIP);
for(int i=0; i<=N; i=i+1){
angulo = i*TWO_PI/N;
radio = r + rango*sin( i*TWO_PI*nciclos/N );
x = radio*cos(angulo);
y = radio*sin(angulo);
// vértice en la base
vertex(x,y,0);
// vértice en la tapa
vertex(x,y,h);
}
endShape();
}3.4 Cilindro con base/tapa periódica y desfasada

Esta función recibe seis parámetros: r para el radio, h para la altura, N para el número de lados en la base/tapa, rango para cuánto puede variar el radio, nciclos para indicar cuántos picos tendrá la base/tapa, y fase para indicar el desfase entre la base y la tapa.
void cilindro(float r, float h, int N, float rango, int nciclos, float fase){
// dibuja un cilindro con base periódica
// r: radio de la base
// h: altura
// N: número de divisiones en la base
// rango: cuánto puede variar el radio hacia arriba y hacia abajo
// nciclos: cuántos ciclos/picos tiene la base
// fase: cuánto está desfasada (en radianes) la tapa de la base
// variables auxiliares
float x,y,angulo,radio;
beginShape(QUAD_STRIP);
for(int i=0; i<=N; i=i+1){
angulo = i*TWO_PI/N;
radio = r + rango*sin( i*TWO_PI*nciclos/N );
x = radio*cos(angulo);
y = radio*sin(angulo);
// vértice en la base
vertex(x,y,0);
radio = r + rango*sin( i*TWO_PI*nciclos/N + fase);
x = radio*cos(angulo);
y = radio*sin(angulo);
// vértice en la tapa
vertex(x,y,h);
}
endShape();
}4 Ejemplos de mallas cónico-cilíndricas
Estas mallas son modificación de las cilíndricas, con la posibilidad de cambiar el radio y/o la forma de la base respecto a la tapa
4.1 Cono-cilindro 1

En esta malla se puede cambiar el radio de la base y de la tapa.
Los parámetros que recibe con: r1 para el radio de la base, r2 para el radio de la tapa, h para la altura, y N para el número de lados en base y tapa.
void cilindroCono(float r1, float r2, float h, int N){
// dibuja un cilindro con base y tapa de diferente radio
// r1: radio de la base
// r2: radio de la tapa
// h: altura
// N: número de divisiones en la base/tapa
// variables auxiliares
float x,y,angulo;
beginShape(QUAD_STRIP);
for(int i=0; i<=N; i++){
angulo = i*TWO_PI/N;
x = r1*cos(angulo);
y = r1*sin(angulo);
// vértice en la base
vertex(x,y,0);
x = r2*cos(angulo);
y = r2*sin(angulo);
// vértice en la tapa
vertex(x,y,h);
}
endShape();
}4.1.1 Variación: rango de ángulos
Esta versión de la función permite especificar el ángulo inicial y final de la figura. Nota que los ángulos son en radianes:
void cilindroCono(float r1, float r2, float h, int N, float anguloInicial, float anguloFinal) {
// dibuja un cilindro con base y tapa de diferente radio
// r1: radio de la base
// r2: radio de la tapa
// h: altura
// N: número de divisiones en la base/tapa
// anguloInicial: a partir de qué ángulo empieza el cilindro (en radianes)
// anguloFinal: en qué ángulo termina el cilindro (en radianes)
// variables auxiliares
float x, y;
beginShape(QUAD_STRIP);
for (float angulo=anguloInicial; angulo<=anguloFinal; angulo += (anguloFinal-anguloInicial)/N) {
x = r1*cos(angulo);
y = r1*sin(angulo);
// vértice en la base
vertex(x, y, 0);
x = r2*cos(angulo);
y = r2*sin(angulo);
// vértice en la tapa
vertex(x, y, h);
}
endShape();
}4.2 Cono-cilindro 2

En esta malla la tapa y la base son figuras periódicas, con diferente radio, rango de cambio de radio, y número de picos/ciclos.
Los parámetros que recibe con: r1 para el radio de la base, r2 para el radio de la tapa, h para la altura, N para el número de lados en base y tapa, rango1 para indicar cuánto cambia el radio de la base, rango2 para indicar cuánto cambia el radio de la tapa, nciclos1 para indicar cuántos picos tiene la base, y nciclos2 para indicar cuántos picos tiene la tapa.
void cilindroCono(float r1, float r2, float h, int N, float rango1, float rango2, int nciclos1, int nciclos2){
// dibuja un cilindro con base y tapa de diferente radio y diferente rango
// r1: radio de la base
// r2: radio de la tapa
// h: altura
// N: número de divisiones en la base/tapa
// rango1: cuánto puede variar el radio de la base hacia arriba y hacia abajo
// rango2: cuánto puede variar el radio de la tapa hacia arriba y hacia abajo
// nciclos1: cuántos ciclos/picos tiene la base
// nciclos2: cuántos ciclos/picos tiene la tapa
// variables auxiliares
float x,y,angulo,radio;
beginShape(QUAD_STRIP);
for(int i=0; i<=N; i++){
angulo = i*TWO_PI/N;
radio = r1 + rango1*sin( i*TWO_PI*nciclos1/N);
x = radio*cos(angulo);
y = radio*sin(angulo);
// vértice en la base
vertex(x,y,0);
radio = r2 + rango2*sin( i*TWO_PI*nciclos2/N);
x = radio*cos(angulo);
y = radio*sin(angulo);
// vértice en la tapa
vertex(x,y,h);
}
endShape();
}