P3D: Retícula

Llamaremos retícula a una malla que consiste en una “red” de vértices.

Una manera de construirla consiste en establecer una serie de QUAD_STRIPs (filas) una al lado de la otra, con vértices en coordenadas x,y separadas de manera uniforme.

Podemos tener una función z(x,y) que de acuerdo a los valores de x,y, regresa el valor de la altura que le corresponde a ese vértice. Esa función z(x,y) la podemos modificar libremente para encontrar distintos resultados.

1 Una posible función “retícula”

La siguiente es una función que dibuja una red de n filas y m columnas de celdas, cada celda con d unidades de lado, y toda centrada en el origen:

void reticula(int n, int m, float d) {
  // n: número de filas
  // m: número de columnas
  // d: longitud del lado de la celda
  float x,y1,y2,z1,z2;
  for (int f=0; f<m; f++) {
    // dibuja una fila
    beginShape(QUAD_STRIP);
    for(int c=0; c<n; c++){
      x = c*d  - n*d/2;
      y1 = f*d - m*d/2;
      y2 = (f+1)*d - m*d/2; 
      z1 = z(x, y1);
      z2 = z(x, y2);
      // vértice de "arriba"
      vertex(x, y1, z1);
      // vértice de "abajo"
      vertex(x, y2, z2);
    }
    endShape();
  }
}

Esta función necesita de una función z que podemos definir de la siguiente forma:

1.1 Función “z”:

Forma básica de la función “z”:

float z(float x, float y){
  // esta función determina el valor que tendrá z
  // para una determinada coordenada x,y
 float z = 1;
 return z; 
}

Podemos leerla como una función que regresa un número de punto flotante (float), que recibe dos parámetros: x, y.

En el caso de arriba, para cualquier valor de x,y, el valor de z es 1, por lo que resulta un plano.

2 Posibilidades a probar

En la función z( x, y ) podemos escribir distintas operaciones en términos de x,y

2.1 Parábolas

Por ejemplo una parábola en términos de y:

float z(float x, float y){
 float z = -0.1*y*y;
 return z; 
}

O una parábola en x,y:

float z(float x, float y){
 float z = -0.1*y*y -0.1*x*x;
 return z; 
}

2.2 Trigonométricas

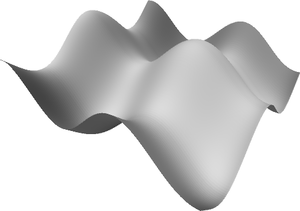
También podemos incluir funciones trigonométricas, por ejemplo combinaciones de funciones sin() y cos():

float z(float x, float y){
 float z = sin(x) + cos(y);
 return z; 
}

[Funciones trigonométricas]

2.3 Más funciones y operadores

Podemos utilizar otras funciones matemáticas:

float z(float x, float y){
 float z = sqrt(x*x + y*y);
 return z; 
}

Operadores aritméticos en general (por ejemplo módulo):

float z(float x, float y){
 float z = y%2;
 return z; 
}

Otro ejemplo con módulo:

float z(float x, float y){
 float z = y%2+x%3;
 return z; 
}

2.4 Combinaciones

Y en general combinaciones que pueden volverse muy complejas:

float z(float x, float y){
 float z = cos(sqrt((x*x + y*y)*10))/exp((x*x+y*y)*0.1);
 return z; 
}

2.5 Condicionales

También podemos utilizar condicionales para realizar cambios que se llamarían no lineales:

float z(float x, float y){
 float z = 1;
 if ( x < 0){
   z = -1;
 }
 return z; 
}

2.6 Combinación de todo

Y bueno, en general combinar todas las opciones:

float z(float x, float y){
 float z = sqrt(x*x + y*y);
 if ( x < 0){
   z = cos(y);
 }
 return z; 
}

Te invito a explorar con diferentes posibilidades - no es necesario saber de antemano qué va a surgir.

3 Programa completo

El programa completo para mostrar una retícula con una función “z” dada, quedaría algo así:

import peasy.*;
PeasyCam cam;
void setup() {
  size(600, 600, P3D);
  cam = new PeasyCam(this, 15);
  perspective(PI/3, 1.0*width/height, 0.1, 100);
}
void draw() {
  background(255);
  ambientLight(50,50,50);
  pointLight(230, 230, 230, 0, 10, 0);
  noStroke();
  reticula(100, 100, 0.1);
}

float z(float x, float y){
  // esta función determina el valor que tendrá z
  // para una determinada coordenada x,y
 float z = sqrt(x*x + y*y);
 if(x<0){
   z = cos(y); 
 }
 return z; 
}

void reticula(int n, int m, float d) {
  // n: número de filas
  // m: número de columnas
  // d: longitud del lado de la celda
  float x,y1,y2,z1,z2;
  for (int f=0; f<n; f++) {
    // dibuja una fila
    beginShape(QUAD_STRIP);
    for(int c=0; c<n; c++){
      x = c*d  - n*d/2;
      y1 = f*d - m*d/2;
      y2 = (f+1)*d - m*d/2; 
      z1 = z(x, y1);
      z2 = z(x, y2);
      // vértice de "arriba"
      vertex(x, y1, z1);
      // vértice de "abajo"
      vertex(x, y2, z2);
    }
    endShape();
  }
}